Among preoder, inorder and postorder binary tree traversal problems, postorder traversal is the most complicated one.
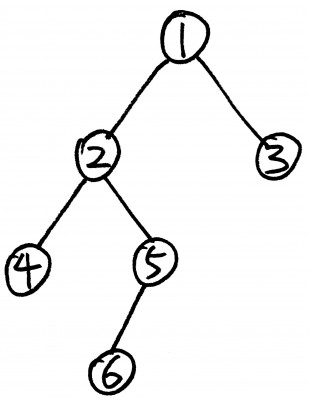
For example, for the following tree, the post order traversal returns {4, 6, 5, 2, 3, 1}.
Java Solution 1
The key to to iterative postorder traversal is the following:
- The order of “Postorder” is: left child -> right child -> parent node.
- Find the relation between the previously visited node and the current node
- Use a stack to track nodes
As we go down the tree to the lft, check the previously visited node. If the current node is the left or right child of the previous node, then keep going down the tree, and add left/right node to stack when applicable. When there is no children for current node, i.e., the current node is a leaf, pop it from the stack. Then the previous node become to be under the current node for next loop. You can using an example to walk through the code.
//Definition for binary tree public class TreeNode { int val; TreeNode left; TreeNode right; TreeNode(int x) { val = x; } } public class Solution { public ArrayList<Integer> postorderTraversal(TreeNode root) { ArrayList<Integer> lst = new ArrayList<Integer>(); if(root == null) return lst; Stack<TreeNode> stack = new Stack<TreeNode>(); stack.push(root); TreeNode prev = null; while(!stack.empty()){ TreeNode curr = stack.peek(); // go down the tree. //check if current node is leaf, if so, process it and pop stack, //otherwise, keep going down if(prev == null || prev.left == curr || prev.right == curr){ //prev == null is the situation for the root node if(curr.left != null){ stack.push(curr.left); }else if(curr.right != null){ stack.push(curr.right); }else{ stack.pop(); lst.add(curr.val); } //go up the tree from left node //need to check if there is a right child //if yes, push it to stack //otherwise, process parent and pop stack }else if(curr.left == prev){ if(curr.right != null){ stack.push(curr.right); }else{ stack.pop(); lst.add(curr.val); } //go up the tree from right node //after coming back from right node, process parent node and pop stack. }else if(curr.right == prev){ stack.pop(); lst.add(curr.val); } prev = curr; } return lst; } } |
Java Solution 2 – Simple!
This solution is simple, but note that the tree’s structure gets changed since children are set to null.
public List<Integer> postorderTraversal(TreeNode root) { List<Integer> res = new ArrayList<Integer>(); if(root==null) { return res; } Stack<TreeNode> stack = new Stack<TreeNode>(); stack.push(root); while(!stack.isEmpty()) { TreeNode temp = stack.peek(); if(temp.left==null && temp.right==null) { TreeNode pop = stack.pop(); res.add(pop.val); } else { if(temp.right!=null) { stack.push(temp.right); temp.right = null; } if(temp.left!=null) { stack.push(temp.left); temp.left = null; } } } return res; } |
true.
this can be achieved using recursion
public List postorderTraversal(TreeNode root) {
List nodeList = new ArrayList();
postorder(root, nodeList);
return nodeList;
}
public void postorder(TreeNode node, List list) {
if(node == null) {
return;
}
postorder(node.left, list);
postorder(node.right, list);
list.add(node.val);
}
Wouldn’t be easier and faster to use HashSet instead of List?
You can keep track of peeked nodes and not break the tree…
Actually we can prevent Tree from breaking, just keep track of peeked nodes. Once peeked can only be poped..
public List postorderTraversal(TreeNode root) {
List results = new ArrayList();
if(root == null){
return results;
}
Stack stack = new Stack();
stack.push(root);
List peeked = new ArrayList();
while(!stack.isEmpty()){
TreeNode curr = stack.peek();
if((curr.left == null && curr.right == null) || peeked.contains(curr)){
results.add(stack.pop().val);
}else{
if(curr.right != null){
stack.push(curr.right);
}
if(curr.left != null){
stack.push(curr.left);
}
peeked.add(curr);
}
}
return results;
}
Try my solution, tested and working :
public ArrayList postorderTraversal(TreeNode a) {
            Stack st = new Stack();
            ArrayList list = new ArrayList();
            while(a != null || !st.isEmpty()){
                        if(a!=null) {
                                    st.push(a);
                                    a = a.left;
                        } else {
                                    if(st.peek().right != null){
                                                a = st.peek().right;
                                                st.peek().right = null;
                                    } else {
                                                list.add(st.pop().val);
                                    }
                        }
            }
            return list;
}
Yes it does, due to the lines left = null/right = null. This simple neat solution must be based on precondition of ‘input tree will a cloned tree of original’
I tried implementing your solution and it works fine for traversal but the problem is that it probably breaks the Tree. The tree doesn’t remain intact as you are making left and right of all nodes as null. Found it while traversing the same tree with Pre-order method.
Binary Tree Postorder Traversal :
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
public class Solution {
public List postorderTraversal(TreeNode root) {
List res = new ArrayList();
if(root==null)
return res;
helper(root,res);
return res;
}
public void helper(TreeNode root,List res){
if(root!=null){
helper(root.left,res);
helper(root.right,res);
res.add(root.val);
}
}
}
Great solution! Thanks!
Your solution is awesome and easier, just keep the object as Integer and not integer. works like a charm.
compiler will report error that the ‘prev’ may be null at that location.
public class Solution {
public List postorderTraversal(TreeNode root) {
List res = new ArrayList();
if(root==null) {
return res;
}
Stack stack = new Stack();
stack.push(root);
while(!stack.isEmpty()) {
TreeNode temp = stack.peek();
if(temp.left==null && temp.right==null) {
TreeNode pop = stack.pop();
res.add(pop.val);
}
else {
if(temp.right!=null) {
stack.push(temp.right);
temp.right = null;
}
if(temp.left!=null) {
stack.push(temp.left);
temp.left = null;
}
}
}
return res;
}
}
Given binary tree {1,#,2,3}, it doesn’t work.
1. push root of 1 into stack
2. c = null
3. t= root of 1
4. list.add(1);
5 stack empty && c==null
I think the solution can be simplified a little by just checking elements that are popped against the current peek of the stack. If the popped element is the left child of the peek, then just point to the right child. If it is the right already, do nothing – the pointer will be null next time and the parent will just be popped and added to the list:
public static void doPostorderTraversal3(List list, TreeNode root){
Stack stack = new Stack();
TreeNode c = root;
while (!stack.isEmpty() || c!=null){
if (c!=null){
stack.push(c);
c = c.left;
} else {
TreeNode t = stack.pop();
list.add(t.val);
if (!stack.empty() && stack.peek().left == t){
c = stack.peek().right;
}
}
}
}
hi this can be simplified in a better way as below
public class TreeNode {
public T data;
public TreeNode LeftChild;
public TreeNode RightChild;
public TreeNode() {
this.data = null;
this.LeftChild = null;
this.RightChild = null;
}
}
public void postOrderTraversal(TreeNode root){
Stack<TreeNode> st = new Stack<TreeNode>();
st.push(root);
TreeNode right = root;
while(!st.empty()){
TreeNode temp = st.peek();
if(temp.LeftChild != null && ((temp.RightChild != right) && (temp.LeftChild != right))){
st.push(temp.LeftChild);
}else{
if(temp.RightChild != null && temp.RightChild != right){
st.push(temp.RightChild);
}else{
right = st.pop();
System.out.print(right.data + “t”);
}
}
}
System.out.print(“n”);
}