Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it is able to trap after raining.
For example, given [0,1,0,2,1,0,1,3,2,1,2,1], return 6.
Analysis
This problem is similar to Candy. It can be solve by scanning from both sides and then get the total.
Java Solution
public int trap(int[] height) { int result = 0; if(height==null || height.length<=2) return result; int left[] = new int[height.length]; int right[]= new int[height.length]; //scan from left to right int max = height[0]; left[0] = height[0]; for(int i=1; i<height.length; i++){ if(height[i]<max){ left[i]=max; }else{ left[i]=height[i]; max = height[i]; } } //scan from right to left max = height[height.length-1]; right[height.length-1]=height[height.length-1]; for(int i=height.length-2; i>=0; i--){ if(height[i]<max){ right[i]=max; }else{ right[i]=height[i]; max = height[i]; } } //calculate totoal for(int i=0; i<height.length; i++){ result+= Math.min(left[i],right[i])-height[i]; } return result; } |
= It can be solve by scanning from both sides and then get the total.
it is not an explanation.
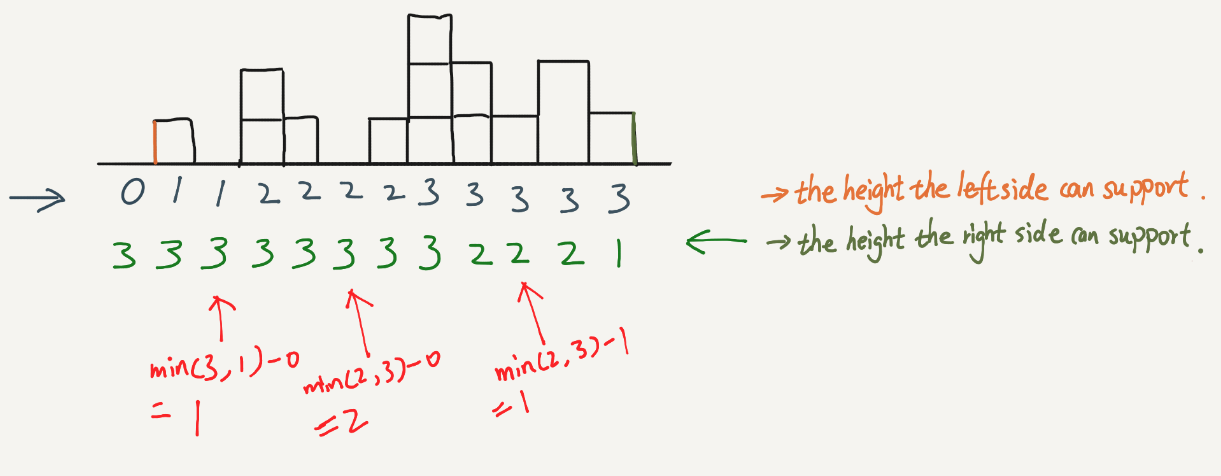
here is explanation:
=1
lets say for indxs 0 and N it is 2 biggest elevation points!
max1 x x x x x maxN
solution is simple, you min( max1, maxN) multiply length of array, and minus all elevations points inside. they all smaller.
=2 lets say it is not.
there is bigger elevation point after max1 (left to right ), and-or bigger elevation point before maxN (from right to left) , we did reduction! calc result for found new max’s on left and right sides and repeat!!
that is it!
this is variation of solution finding closest bigger element for array element to left or right!
I found that solution is very popular and helpful : https://www.youtube.com/watch?v=WOO27cP8rN4
Check out this solution: https://qr.ae/pGGvzZ
class Solution {
public:
int trap(vector& height) {
// maxLeft[i] = max height to the left of i
// maxRight[i] = max height to the right of i
vector maxLeft(height.size()), maxRight(height.size());
if(height.size() == 0) return 0;
maxLeft[0] = height[0];
maxRight[height.size() - 1] = height[height.size() - 1];
for(int i = 1, j = height.size() - 2; i = 0; i++, j--) {
maxLeft[i] = max(maxLeft[i - 1], height[i]);
maxRight[j] = max(maxRight[j + 1], height[j]);
}
int ans = 0;
for(int i = 0; i < height.size(); i++) {
int minFromTwoSides = min(maxLeft[i], maxRight[i]);
ans += max(minFromTwoSides - height[i], 0);
}
return ans;
}
};
My solution in Javascript (the relevant part):
function calcLeftSideSupport(inputArray){
let resultArray = [];
let tempMax = 0;
for(let i=0; i= tempMax){
tempMax = inputArray[i];
}
resultArray[i] = tempMax;
}
return resultArray;
}
function calcRightSideSupport(inputArray){
let resultArray = [];
let tempMax = 0;
for(let i=inputArray.length-1; i>=0;i--){
if (inputArray[i] >= tempMax){
tempMax = inputArray[i];
}
resultArray[i] = tempMax;
}
return resultArray;
};
function calcRainCapacity(originalArray, leftArray, rightArray){
let rainCapacity = 0;
let rainArray = [];
for(let i=0;i<originalArray.length;i++){
rainArray[i]= Math.min(leftArray[i],rightArray[i]) - originalArray[i];
rainCapacity += rainArray[i];
}
return [rainCapacity,rainArray];
}
function calcMaxHeight(numberArray){let tempArray = numberArray.slice();
let maxHeight = tempArray.sort(function(a, b){return b-a})[0];
return maxHeight;
}
You can use given heights array to calculate it, firstly see my c++ solution above by using one array instead of two arrays, then you can reuse heights by start from two ends.
int Water::trapping(const vector& heights) {
if (heights.size() < 2) {
return 0;
}
vector heights;
heights.push_back(heights[0]);
for (int i = 1; i = 0; i--) {
int m = i == heights.size() - 1 ? heights[i] : max(heights[i], heights[i + 1]);
heights[i] = min(heights[i], m);
}
int t = 0;
for (int i = 1; i < heights.size(); i++) {
t += min(heights[i], heights[i - 1]);
}
return t;
}
This is a pretty cool solution. Thanks for sharing.
public class Solution {
public int trap(int[] height) {
if(height == null || height.length==0) return 0;
int leftMax = 0, rightMax = 0, left = 0, max = 0;
int right = height.length-1;
while(left height[left] ? leftMax : height[left];
rightMax = rightMax > height[right] ? rightMax : height[right];
max += leftMax < rightMax ? leftMax - height[left++] : rightMax - height[right--];
}
return max;
}
}
public class Solution {
public int trap(int[] height) {
int l = height.length;
if(l < 3) return 0;
int[] leftMax = new int[l];
int[] rightMax = new int[l];
int maxL = height[0];
int maxR = height[l-1];
for(int i = 0; i maxL ? height[i] : maxL;
leftMax[i] = maxL;
maxR = height[l-1-i] > maxR ? height[l-1-i] : maxR;
rightMax[l-1-i] = maxR;
}
int waterTrapped = 0;
for(int i = 0; i rightMax[i] ? rightMax[i] - height[i] : leftMax[i] - height[i];
}
return waterTrapped;
}
}
Constant O(1) space and O(n) time.
public class Solution {
public int trap(int[] height) {
if (height == null || height.length < 3)
return 0;
int result = 0;
int left = 0;
int right = height.length - 1;
int maxLeft = 0;
int maxRight = 0;
int curHeight;
while (left < right) {
curHeight = Math.min(maxLeft, maxRight);
if (maxLeft < maxRight) {
result += Math.max(curHeight - height[left], 0);
maxLeft = Math.max(height[left], maxLeft);
left++;
}
else {
result += Math.max(curHeight - height[right], 0);
maxRight = Math.max(height[right], maxRight);
right--;
}
}
curHeight = Math.min(maxLeft, maxRight);
result += Math.max(curHeight - height[right], 0);
return result;
}
}
sorry….my mistake….I meant constant space….
Is it possible to do it in constant time? it’s a FB interview question. Haven’t figured out how to do it…