Quicksort Array in Java

by

Quicksort is a divide and conquer algorithm. It first divides a large list into two smaller sub-lists and then recursively sort the two sub-lists. If we want to sort an array without any extra space, quicksort is a good option. On average, time complexity is O(n log(n)).

The basic step of sorting an array are as follows:

  • Select a pivot
  • Move smaller elements to the left and move bigger elements to the right of the pivot
  • Recursively sort left part and right part

This post shows two versions of the Java implementation. The first one picks the rightmost element as the pivot and the second one picks the middle element as the pivot.

Version 1: Rightmost element as pivot

The following is the Java Implementation using rightmost element as the pivot.

public class QuickSort {
 
    public static void main(String[] args) {
        int[] arr = {4, 5, 1, 2, 3, 3};
        quickSort(arr, 0, arr.length-1);
        System.out.println(Arrays.toString(arr));
    }
 
    public static void quickSort(int[] arr, int start, int end){
 
        int partition = partition(arr, start, end);
 
        if(partition-1>start) {
            quickSort(arr, start, partition - 1);
        }
        if(partition+1<end) {
            quickSort(arr, partition + 1, end);
        }
    }
 
    public static int partition(int[] arr, int start, int end){
        int pivot = arr[end];
 
        for(int i=start; i<end; i++){
            if(arr[i]<pivot){
                int temp= arr[start];
                arr[start]=arr[i];
                arr[i]=temp;
                start++;
            }
        }
 
        int temp = arr[start];
        arr[start] = pivot;
        arr[end] = temp;
 
        return start;
    }
}

You can use the example below to go through the code.

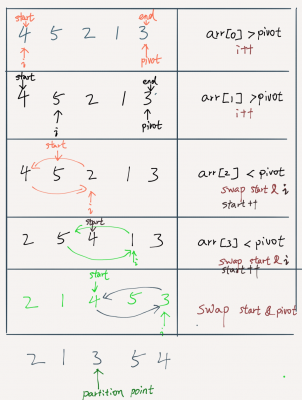
Version 2: Middle element as pivot

public class QuickSort {
	public static void main(String[] args) {
		int[] x = { 9, 2, 4, 7, 3, 7, 10 };
		System.out.println(Arrays.toString(x));
 
		int low = 0;
		int high = x.length - 1;
 
		quickSort(x, low, high);
		System.out.println(Arrays.toString(x));
	}
 
	public static void quickSort(int[] arr, int low, int high) {
		if (arr == null || arr.length == 0)
			return;
 
		if (low >= high)
			return;
 
		// pick the pivot
		int middle = low + (high - low) / 2;
		int pivot = arr[middle];
 
		// make left < pivot and right > pivot
		int i = low, j = high;
		while (i <= j) {
			while (arr[i] < pivot) {
				i++;
			}
 
			while (arr[j] > pivot) {
				j--;
			}
 
			if (i <= j) {
				int temp = arr[i];
				arr[i] = arr[j];
				arr[j] = temp;
				i++;
				j--;
			}
		}
 
		// recursively sort two sub parts
		if (low < j)
			quickSort(arr, low, j);
 
		if (high > i)
			quickSort(arr, i, high);
	}
}

Output:

9 2 4 7 3 7 10
2 3 4 7 7 9 10

Here is a very good animation of quicksort.

27 thoughts on “Quicksort Array in Java”

  1. With respect to Version 1: To avoid unnecessary swap, in the function partition we can add the below check :
    int temp = arr[start];
    if(temp != pivot){
    arr[start] = pivot;
    arr[end] = temp;
    }

  2. The code given up produces a StackOverflow Error, and it does not compile. Can someone suggest why that might be the reason? If you change the test array, the correct output is not shown.

  5. @Sorter

    if (arr == null || arr.length == 0)
    return;
    i would write in main:
    if( x.length != 0 )

    This would be a null pointer exception if x is null, hence a null check is required. As a stand-alone program it doesn’t matter, because you already know the inputs are good, but it’s good practice to handle it anyway.

    But I would actually use arr.length > 1 is even faster

    This is a misconception. Perhaps this was true decades ago, but the compiler knows that a division by 2 is equivalent to a bit shift by 1. Same with multiplication. It’s easy to do a benchmark, or just examine the Java byte code and you’ll see it’s the same.

    AKA, don’t do this, because it may be confusing for developers who come behind you who may not recognize that the bit shift is division/multiplication.

    @kk
    I could be wrong but I think the running time for the partition part could be O(n^2) so this Quicksort does not have O(nlgn) running time.

    This is sort of true. The worst case runtime of quicksort is n^2, but on average it is nlgn, so we say it is nlgn.

  6. And instead of:
    int middle = low + (high – low) / 2;
    int pivot = arr[middle];
    i would write:
    int pivot = arr[ (high + low ) / 2];

    Because i have knowledge in math, i can make your math expression less complicate for you:
    low + (high – low) / 2
    = low + high/2 – low/2
    = ( low – low/2 ) + high/2
    = low/2 + high/2
    = (low + high) / 2

  7. And instead of:
    int middle = low + (high – low) / 2;
    int pivot = arr[middle];
    i would write:
    int pivot = arr[ (high + low ) / 2];

    Because i have knowledge in math, i can make your math expression less complicate for you:
    low + (high – low) / 2
    = low + high/2 – low/2
    = ( low – low/2 ) + high/2
    = low/2 + high/2
    = (low + high) / 2

  8. Instead of the first line in your quickSort:
    if (arr == null || arr.length == 0)
    return;
    i would write in main:
    if( x.length != 0 )
    {
    quickSort(x, low, high);
    System.out.println(Arrays.toString(x));
    }

  9. Running time is N log N for the average input.
    Each recursion runs log N (average) times, and each run is bounded to N

  11. Doesn’t one of the pivot conditionals need to have an equals, such as =, instead of ? Otherwise, what happens if the pivot value occurs multiple times in the array?

  12. try this

    public void quickSort(int[] arr, int p, int r){

    if(p < r) {

    int q = partition(arr, p, r);

    quickSort(arr, p, q-1);

    quickSort(arr, q+1, r);

    }

    }

    public int partition(int arr[], int p, int r)

    {

    int i = p-1;

    int pivot = arr[r];

    for (int j = p; j <= r; j++) {

    if(arr[j] <= pivot){

    i++;

    //do the swap

    if(i!=j){

    arr[i] = arr[i] ^ arr[j];

    arr[j] = arr[i] ^ arr[j];

    arr[i] = arr[i] ^ arr[j];

    }

    }

    }

    return i;

    }

  15. I could be wrong but I think the running time for the partition part could be O(n^2) so this Quicksort does not have O(nlgn) running time.

  16. Can we remove the if conditions here :

    if (low i)

    quickSort(arr, i, high);

    Inside the function we are again checking the same.

  18. In recursively sort two sub parts, it seems you don’t need to check relationship between low and j (high and i) before you call quickSort. Since you define a stop condition of low>=high at the beginning.

  22. ah no? He’s referring to get the difference first: (high – low), then use this divided by 2, then add to the starting position, which “low+” will be the last operation.

  23. I just wanted to understand one point.The above quickSort method excluding the recursion part modifies the array such that all elements less than pivot are on left side and all elements greater than pivot are on right side.Is this correct.My point is that the pivot will not be at the boundary but it will be somewhere in the right part ?

  24. Just a little problem with your statement. You mean to say they will not retain their *order* after sorting. Not places.

  26. Quicksort is slightly sensitive to input that happens to be in the right order, in which case it can skip some swaps. Mergesort doesn’t have any such optimizations, which also makes Quicksort a bit faster compared to Mergesort.

    To know more about quicksort and mergesort, below link can be useful

    Why Quick sort is better than Merge sort

Leave a Comment