LeetCode – Combination Sum (Java)

 

Given a set of candidate numbers (C) and a target number (T), find all unique combinations in C where the candidate numbers sums to T. The same repeated number may be chosen from C unlimited number of times.

Note: All numbers (including target) will be positive integers. Elements in a combination (a1, a2, ... , ak) must be in non-descending order. (ie, a1 <= a2 <= ... <= ak). The solution set must not contain duplicate combinations. For example, given candidate set 2,3,6,7 and target 7, A solution set is: 

[7] 
[2, 2, 3]

Java Solution

The first impression of this problem should be depth-first search(DFS). To solve DFS problem, recursion is a normal implementation.

The following example shows how DFS works:

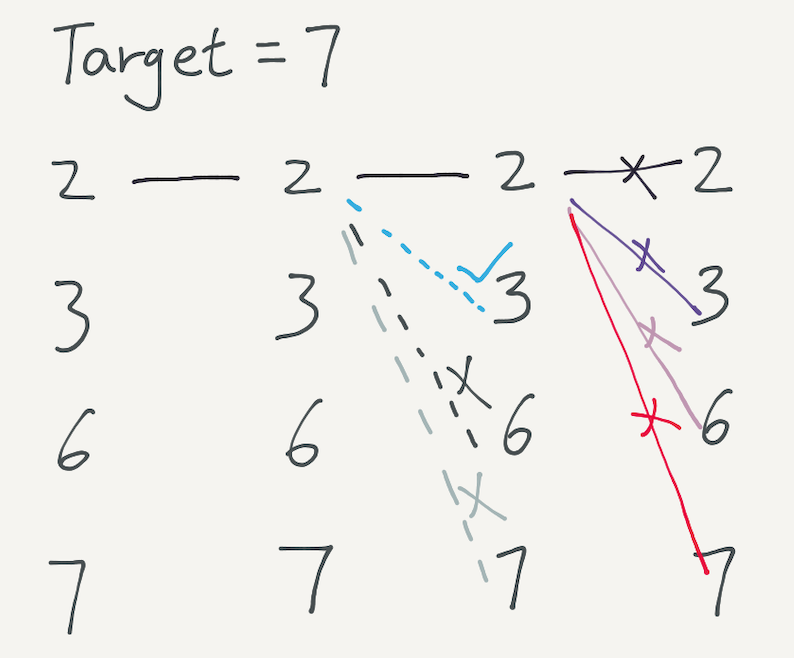
public List<List<Integer>> combinationSum(int[] candidates, int target) {
    List<List<Integer>> result = new ArrayList<>();
    List<Integer> temp = new ArrayList<>();
    helper(candidates, 0, target, 0, temp, result);
    return result;
}
 
private void helper(int[] candidates, int start, int target, int sum,
                    List<Integer> list, List<List<Integer>> result){
    if(sum>target){
        return;
    }
 
    if(sum==target){
        result.add(new ArrayList<>(list));
        return;
    }
 
    for(int i=start; i<candidates.length; i++){
        list.add(candidates[i]);
        helper(candidates, i, target, sum+candidates[i], list, result);
        list.remove(list.size()-1);
    }
}

Related posts:

  1. LeetCode – Combination Sum II (Java)
  2. LeetCode – Combination Sum IV (Java)
  3. LeetCode – Super Ugly Number (Java)
  4. LeetCode – Combination Sum III (Java)
Category >> Algorithms  
If you want someone to read your code, please put the code inside <pre><code> and </code></pre> tags. For example: 
<pre><code> 
String foo = "bar";
</code></pre>
  • Rahul Jain

    Hi Guys
    I made a small video explaining the recursion and backtracking concept. Please check out the video
    https://www.youtube.com/watch?v=fL0uPiNHGnw

  • Alik Elzin

    I think the solution would break on [2,2], 4
    The result will have several lists with the same elements – [2,2] – breaks the instruction of “The solution set must not contain duplicate combinations”.

  • TISHANT CHANDRAKAR

    Just add this line in place of if(target==0),
    (target==0 && result.contains(curr))

  • Derek

    This solution doesn’t handle duplicate numbers in the list. Duplicates should be stripped out or logic needs to account for it.

  • pjpal

    What would be the running time of this algorithm?

  • Александр Ефремов

    Because this is the main idea of backtracking – try option (curr.add(candidate)), then backtrack – curr.remove(cur.size()-1)

  • Didier

    This solution is incorrect. If candidates are [2, 3, 3, 6, 7]. The returned lists would be:
    [2, 2, 3]
    [2, 2, 3]
    [7]

    May need to add some condition to exclude the repeated entry in candidates.

  • gowtham Bk

    Why can’t we just add curr to result ? Why do we use temp ?

  • ryanlr

    I don’t think so, because duplicates are allowed in a combination set, i. e., the same number csn be used twice.

  • divya

    Shouldn’t it be i+1, 3rd parameter here->combinationSum(candidates, target – candidates[i], i, curr, result);

  • Surbhi Motghare

    Great solution. why are we removing the last element from curr. (last line where curr.remove(curr.size()-1) ? )

  • Dexter

    public static void sum(int[] set,int s){

    int [][]dp = new int[s+1][set.length];

    for(int i=0;i < set.length; i++){

    for(int j = 0; j j){

    dp[j][i] = 0;

    continue;

    }

    if(set[i] == j){

    dp[j][i] = i+1;

    continue;

    }

    int remaining = j-set[i];

    int k = i;

    while(k >= 0){

    if(dp[remaining][k] > 0){

    dp[j][i] = k+1;

    break;

    }

    k–;

    }

    }

    }

    int l=0;

    while(l 0){

    int sum = s;

    int col = l;

    System.out.print(“[“);

    while(sum > 0){

    System.out.print(set[col]+”,”);

    int temp = col;

    col = dp[sum][col]-1;

    sum -= set[temp];

    }

    System.out.print(“]”);

    }

    l++;

    System.out.println(“”);

    }

    }

  • Jeffrey Ni

    Java always pass parameters by value. Here curr is a refferrece to the array object, if you don’t copy it but add it to the result directly, later when you modify curr, it will change the list inside result. You may end up with all same lists in result. You can self-test it.

  • Lean Lee

    I wonder why we need make a temp ArrayList and then copy the curr Arraylist and then add temp into result, why just add curr into the result directly?