LeetCode – Partition to K Equal Sum Subsets (Java)

by

Given an array of integers nums and a positive integer k, find whether it’s possible to divide this array into k non-empty subsets whose sums are all equal.

Example 1:

Input: nums = [4, 3, 2, 3, 5, 2, 1], k = 4
Output: True
Explanation: It’s possible to divide it into 4 subsets (5), (1, 4), (2,3), (2,3) with equal sums.

Java Solution

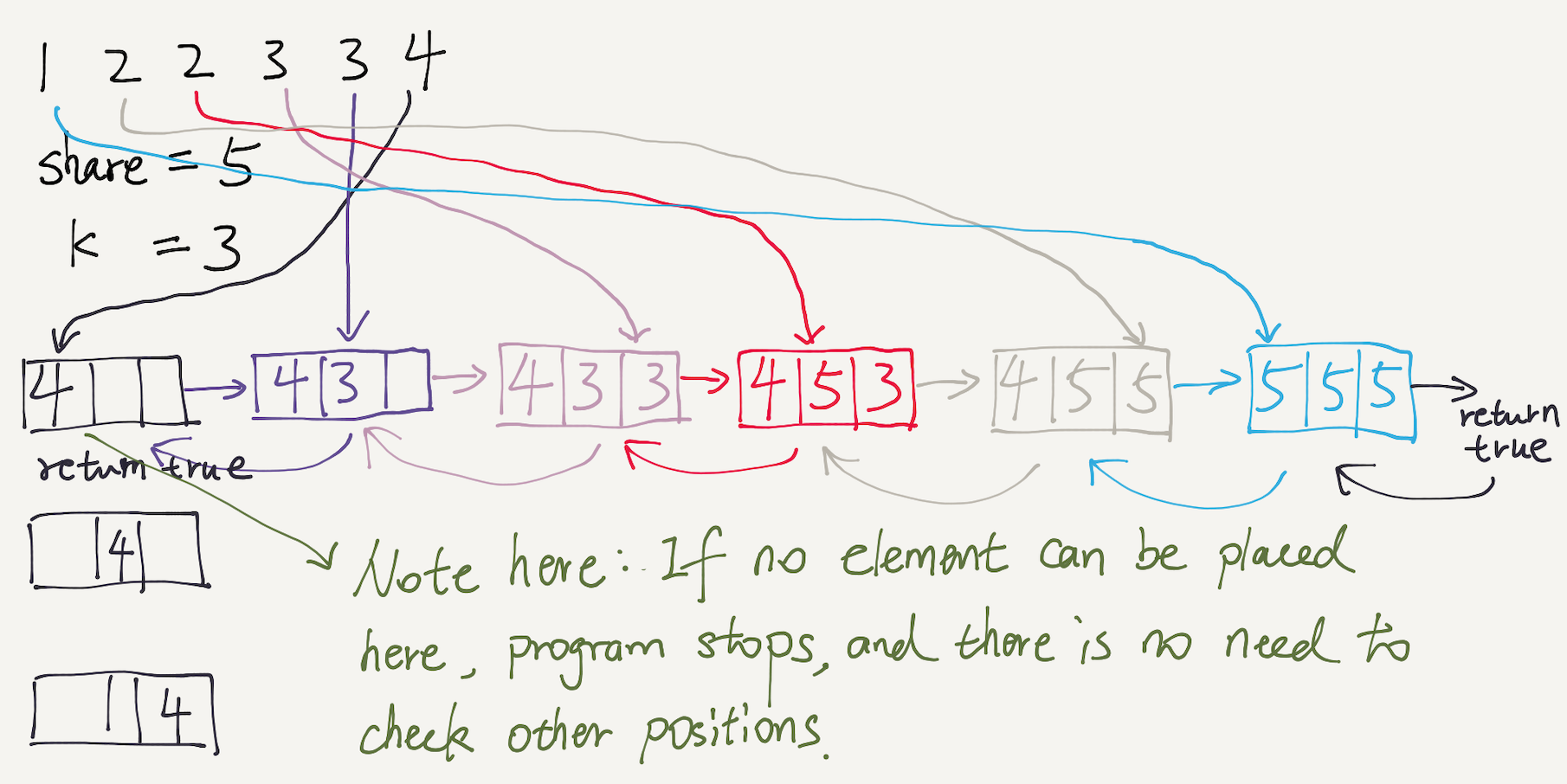
The easiest solution to this problem is DFS. We try to place each element to one of the bucket. The following is a Java solution and there is a diagram to show the execution of the helper() method using the given example. Note the improvement in the for loop.

public boolean canPartitionKSubsets(int[] nums, int k) {
    int sum = 0;
    for(int num: nums){
        sum+=num;
    }
    if(sum%k!=0){
        return false;
    }
 
    int share = sum/k;
 
    //sort array
    Arrays.sort(nums);
 
    int j=nums.length-1;
    if(nums[j]>share){
        return false;
    }
    while(j>=0 && nums[j]==share){
        j--;
        k--;
    }
 
    int[] buckets = new int[k];
    return helper(j, nums, share, buckets);
}
 
//put jth number to each bucket and recursively search
public boolean helper(int j, int[] nums, int share, int[] buckets){
    if(j<0){
        return true;
    }
 
    for(int i=0; i<buckets.length; i++){
        if(buckets[i]+nums[j]<=share){
            buckets[i]+=nums[j];
            if(helper(j-1, nums, share, buckets)){
                return true;
            }
            buckets[i]-=nums[j];
        }
 
        if(buckets[i]==0)  break;//
    }
 
    return false;
}

Leave a Comment