Given an array of non-negative integers, you are initially positioned at the first index of the array. Each element in the array represents your maximum jump length at that position. Determine if you are able to reach the last index. For example: A = [2,3,1,1,4], return true. A = [3,2,1,0,4], return false.
Analysis
We can track the maximum index that can be reached. The key to solve this problem is to find: 1) when the current position can not reach next position (return false) , and 2) when the maximum index can reach the end (return true).
The largest index that can be reached is: i + A[i].
Here is an example:
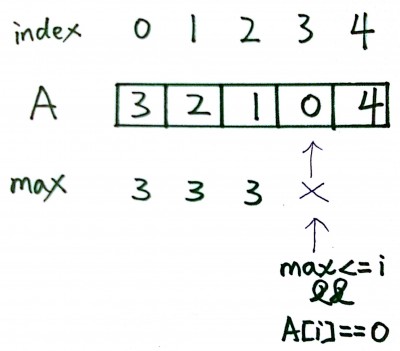
Java Solution
public boolean canJump(int[] A) { if(A.length <= 1) return true; int max = A[0]; //max stands for the largest index that can be reached. for(int i=0; i<A.length; i++){ //if not enough to go to next if(max <= i && A[i] == 0) return false; //update max if(i + A[i] > max){ max = i + A[i]; } //max is enough to reach the end if(max >= A.length-1) return true; } return false; } |
A bit cleaner solution, without checking `
==0` and with using `max()` method.Because the index is representing the distance we already covered and the arr[i] at that position represent the distance we move forward so if the maximum distance covered is same as the index it means that we are maximum at that position and if arr[i] is 0 means we cant move forward so return 0;
beautiful code loved it:)
if A[i]=3 we can jump on i+1, i+2 or i+3. As we are iterating through i, max<=i means that we've reached the last accessible node – cannot jump further, ant current value is 0, meaning that if we do jump on that step, we'll stay there.
is this code right
public static boolean canJump(int[] A) {
if (A.length <= 1) {
return true;
}
int max = A[0]; //max stands for the largest index that can be reached
for (int i = 0; i = A.length – 1) {
return true;
}
//if not enough to go to next
if (i != A.length-1 && A[i] == 0) {
return false;
}
max = i + A[i];
}
return false;
}
in ” if(max <= i && A[i] == 0)
return false;"
why we use "max<=i" ?
Shorter code:
if(a.get(0)==0 && a.size()==1)
return 1;
if(a.get(0)==0)
return 0;
int max=a.get(0);
for(int i=1;i=i)
max=Math.max(max,i+a.get(i));
if(max>=a.size())
return true;
}
return false;
public class Solution {
public boolean canJump(int[] nums) {
if ( nums == null ) return false;
int reach = 0;
for ( int i = 0 ; i < nums.length; i++ ) {
if ( reach < i ) return false;
reach = Math.max(reach, nums[i] + i);
}
return true;
}
Clear code solution and explanation!
use dynamic programming way to solve it:
public class Solution {
public boolean canJump(int[] nums) {
int[] res = new int[nums.length];
res[0] = nums[0];
if(res[0] == 0 && nums.length != 1)return false;
for(int i=1;i<nums.length;i++){
res[i] = Math.max(nums[i],res[i-1]-1);
if(res[i]==0 && i !=nums.length-1)return false;
}
return true;
}
}
The above code does not work. For example:
{ 2, 3, 0, 0, 4 };
If you start from index 0, you can reach 2 and then, you cannot move forward. The above code will return true assuming that you start from 1. We can just work our way from index 0 and see if we reach the end.