LeetCode – Populating Next Right Pointers in Each Node (Java)

Given the following perfect binary tree,

After calling your function, the tree should look like:

         1 -> NULL
       /  \
      2 -> 3 -> NULL
     / \  / \
    4->5->6->7 -> NULL

Java Solution 1 - Simple

public void connect(TreeLinkNode root) {
    if(root==null)
        return;
 
    LinkedList<TreeLinkNode> nodeQueue = new LinkedList<TreeLinkNode>();
    LinkedList<Integer> depthQueue = new LinkedList<Integer>();
 
    if(root!=null){
        nodeQueue.offer(root);
        depthQueue.offer(1);
    }
 
    while(!nodeQueue.isEmpty()){
        TreeLinkNode topNode = nodeQueue.poll();
        int depth = depthQueue.poll();
 
        if(depthQueue.isEmpty()){
            topNode.next = null;
        }else if(depthQueue.peek()>depth){
            topNode.next = null;
        }else{
            topNode.next = nodeQueue.peek();
        }
 
        if(topNode.left!=null){
            nodeQueue.offer(topNode.left);
            depthQueue.offer(depth+1);
        }
 
        if(topNode.right!=null){
            nodeQueue.offer(topNode.right);
            depthQueue.offer(depth+1);
        }        
    }
}

Java Solution 2

This solution is easier to understand. You can use the example tree above to walk through the algorithm. The basic idea is have 4 pointers to move towards right on two levels (see comments in the code).

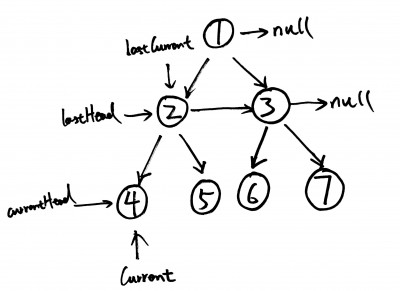
populating-next-right-pointers-in-each-node

public void connect(TreeLinkNode root) {
    if(root == null) 
        return;
 
    TreeLinkNode lastHead = root;//prevous level's head 
    TreeLinkNode lastCurrent = null;//previous level's pointer
    TreeLinkNode currentHead = null;//currnet level's head 
    TreeLinkNode current = null;//current level's pointer
 
    while(lastHead!=null){
        lastCurrent = lastHead;
 
        while(lastCurrent!=null){
            if(currentHead == null){
                currentHead = lastCurrent.left;
                current = lastCurrent.left;
            }else{
                current.next = lastCurrent.left;
                current = current.next;
            }
 
            if(currentHead != null){
                current.next = lastCurrent.right;
                current = current.next;
            }
 
            lastCurrent = lastCurrent.next;
        }
 
        //update last head
        lastHead = currentHead;
        currentHead = null;
    }
 
}

If you want someone to read your code, please put the code inside <pre><code> and </code></pre> tags. For example:

<pre><code> 
String foo = "bar";
</code></pre>

Hooman

in your first solution that second if statement ( if(root!=null) ) is redundent.
Shivam Maharshi

But that would not be constant extra space. It would require O(log(n)) space where n are the number of nodes in the tree. The question specifically mentions no extra space.
Rishabh Jain

Thanks for the solution!
Radu Ionescu

I came up with this solution which seems more easily understandable.

public void connect(TreeLinkNode root) {
// only in edge case where there is no tree
if (root == null) return;

//By induction this will be the leftmost node in the current level
TreeLinkNode cur = root;

//By induction this will be the leftmost node in the next level
TreeLinkNode left = root.left;

//check if this is the last level
if (left == null) return;

//tranverse the current level linking all nodes in the next level
while(cur != null){
//link left and right child of the current node
cur.left.next = cur.right;

//link right child of current node and left child of next node
if (cur.next != null){
cur.right.next = cur.next.left;
}

//progress
cur = cur.next;
}

//move to next level
connect(left);

}
CRH

Do a typical level by level binary tree traversal using a queue. When you encounter that the level is changed, navigate from the queue and update next pointers.

LeetCode – Populating Next Right Pointers in Each Node (Java)

Related posts: