LeetCode – Contains Duplicate III (Java)

by

Given an array of integers, find out whether there are two distinct indices i and j in the array such that the difference between nums[i] and nums[j] is at most t and the difference between i and j is at most k.

Java Solution 1 – Simple

This solution simple. Its time complexity is O(nlog(k)).

public boolean containsNearbyAlmostDuplicate(int[] nums, int k, int t) {
    if(nums==null||nums.length<2||k<0||t<0)
        return false;
 
    TreeSet<Long> set = new TreeSet<Long>();
    for(int i=0; i<nums.length; i++){
        long curr = (long) nums[i];
 
        long leftBoundary = (long) curr-t;
        long rightBoundary = (long) curr+t+1; //right boundary is exclusive, so +1
        SortedSet<Long> sub = set.subSet(leftBoundary, rightBoundary);
        if(sub.size()>0)
            return true;
 
        set.add(curr);   
 
        if(i>=k){ // or if(set.size()>=k+1)
            set.remove((long)nums[i-k]);
        }
    }
 
    return false;
}

Java Solution 2 – Deprecated

The floor(x) method returns the greatest value that is less than x. The ceiling(x) methods returns the least value that is greater than x. The following is an example.
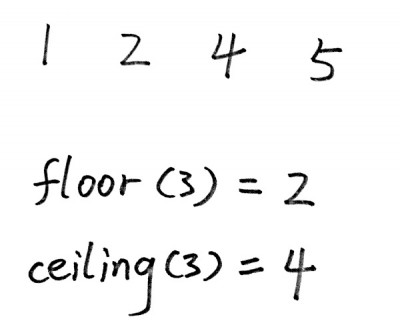
contains-duplicate-iii

public boolean containsNearbyAlmostDuplicate(int[] nums, int k, int t) {
	if (k < 1 || t < 0)
		return false;
 
	TreeSet<Integer> set = new TreeSet<Integer>();
 
	for (int i = 0; i < nums.length; i++) {
		int c = nums[i];
		if ((set.floor(c) != null && c <= set.floor(c) + t)
		|| (set.ceiling(c) != null && c >= set.ceiling(c) -t))
			return true;
 
		set.add(c);
 
		if (i >= k)
			set.remove(nums[i - k]);
	}
 
	return false;
}

5 thoughts on “LeetCode – Contains Duplicate III (Java)”

  1. Isn’t sub.size() = O(k) ? So, O(n*k) not O(n*logk)?

    Looking to the Java 1.8.77 code: fromStart and toEnd are false, therefore it will iterate thu the set => linear.

    abstract class EntrySetView extends AbstractSet<Map.Entry> {
    private transient int size = -1, sizeModCount;

    public int size() {
    if (fromStart && toEnd)
    return m.size();
    if (size == -1 || sizeModCount != m.modCount) {
    sizeModCount = m.modCount;
    size = 0;
    Iterator i = iterator();
    while (i.hasNext()) {
    size++;
    i.next();
    }
    }
    return size;
    }

    It seems to me this is linear.

  5. Hi,
    I admire your excellent solution and posts.
    But I believe there is a possible pitfall for your first solution.

    The possible problematic snippet is:
    set.add(c);
    if (i >= k)
    set.remove(nums[i – k]);
    This would wrongly delete the nums[i], if nums[i] and nums[i – k] have the same value.
    Considering following case:
    Input:
    nums = [1, 50, 70, 90, 110, 1, 2]
    k = 5
    t = 1
    Using the above logic, when we reach i = 5.
    set. add (5)
    set.remove(5)
    Thus the return for this input is false. Actually it should be true. Cause num[5] = 1, num[6] = 2 meet the requirement.
    The possible fix could be:
    if (i >= k)
    set.remove(nums[i – k]);
    set.add((long) nums[j]);

Leave a Comment