LeetCode – Trapping Rain Water (Java)

Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it is able to trap after raining.

For example, given [0,1,0,2,1,0,1,3,2,1,2,1], return 6.

Analysis

This problem is similar to Candy. It can be solve by scanning from both sides and then get the total.

Java Solution

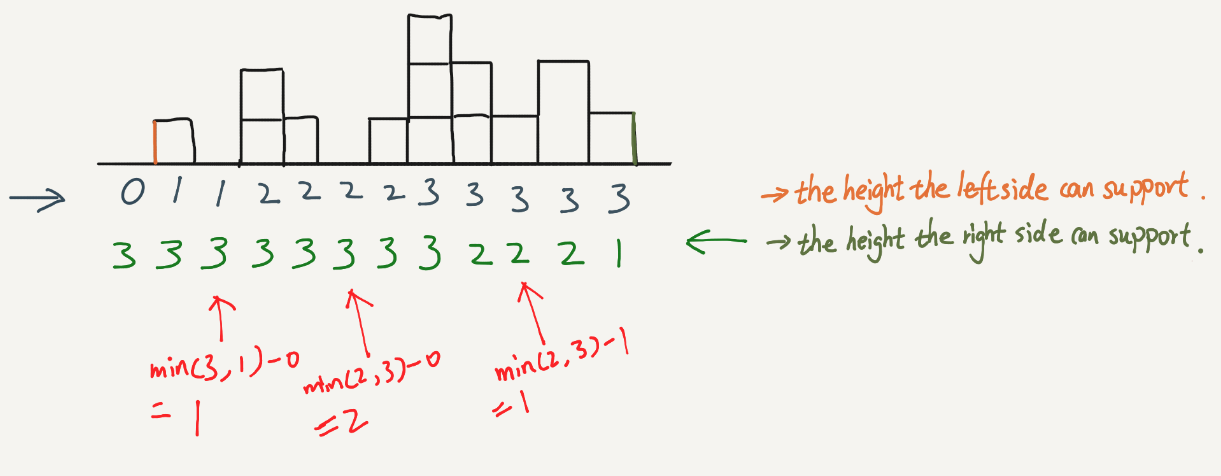
public int trap(int[] height) {
    int result = 0;
 
    if(height==null || height.length<=2)
        return result;
 
    int left[] = new int[height.length];
    int right[]= new int[height.length];
 
    //scan from left to right
    int max = height[0];
    left[0] = height[0];
    for(int i=1; i<height.length; i++){
        if(height[i]<max){
            left[i]=max;
        }else{
            left[i]=height[i];
            max = height[i];
        }
    }
 
    //scan from right to left
    max = height[height.length-1];
    right[height.length-1]=height[height.length-1];
    for(int i=height.length-2; i>=0; i--){
        if(height[i]<max){
            right[i]=max;
        }else{
            right[i]=height[i];
            max = height[i];
        }
    }
 
    //calculate totoal
    for(int i=0; i<height.length; i++){
        result+= Math.min(left[i],right[i])-height[i];
    }
 
    return result;
}

If you want someone to read your code, please put the code inside <pre><code> and </code></pre> tags. For example:

<pre><code> 
String foo = "bar";
</code></pre>

Ali Awan

I found that solution is very popular and helpful : https://www.youtube.com/watch?v=WOO27cP8rN4
Techie Express

Check out this solution: https://qr.ae/pGGvzZ
Amr Hendy

class Solution { public: int trap(vector& height) { // maxLeft[i] = max height to the left of i // maxRight[i] = max height to the right of i vector maxLeft(height.size()), maxRight(height.size()); if(height.size() == 0) return 0; maxLeft[0] = height[0]; maxRight[height.size() - 1] = height[height.size() - 1]; for(int i = 1, j = height.size() - 2; i = 0; i++, j--) { maxLeft[i] = max(maxLeft[i - 1], height[i]); maxRight[j] = max(maxRight[j + 1], height[j]); } int ans = 0; for(int i = 0; i < height.size(); i++) { int minFromTwoSides = min(maxLeft[i], maxRight[i]); ans += max(minFromTwoSides - height[i], 0); } return ans; } };
Ujvári Bálint

My solution in Javascript (the relevant part):
function calcLeftSideSupport(inputArray){ let resultArray = []; let tempMax = 0;
for(let i=0; i= tempMax){ tempMax = inputArray[i]; } resultArray[i] = tempMax; } return resultArray; } function calcRightSideSupport(inputArray){ let resultArray = []; let tempMax = 0; for(let i=inputArray.length-1; i>=0;i--){ if (inputArray[i] >= tempMax){ tempMax = inputArray[i]; } resultArray[i] = tempMax; } return resultArray; }; function calcRainCapacity(originalArray, leftArray, rightArray){ let rainCapacity = 0; let rainArray = []; for(let i=0;i<originalArray.length;i++){ rainArray[i]= Math.min(leftArray[i],rightArray[i]) - originalArray[i]; rainCapacity += rainArray[i]; } return [rainCapacity,rainArray]; }
function calcMaxHeight(numberArray){ let tempArray = numberArray.slice(); let maxHeight = tempArray.sort(function(a, b){return b-a})[0]; return maxHeight; }
Tristan Yan

You can use given heights array to calculate it, firstly see my c++ solution above by using one array instead of two arrays, then you can reuse heights by start from two ends.
Tristan Yan

int Water::trapping(const vector& heights) { if (heights.size() < 2) { return 0; } vector heights;
heights.push_back(heights[0]); for (int i = 1; i = 0; i--) { int m = i == heights.size() - 1 ? heights[i] : max(heights[i], heights[i + 1]); heights[i] = min(heights[i], m); } int t = 0; for (int i = 1; i < heights.size(); i++) { t += min(heights[i], heights[i - 1]); }
return t; }
Yinglei Zhang

This is a pretty cool solution. Thanks for sharing.
Sim Prodigy

public class Solution { public int trap(int[] height) { if(height == null || height.length==0) return 0; int leftMax = 0, rightMax = 0, left = 0, max = 0; int right = height.length-1; while(left height[left] ? leftMax : height[left]; rightMax = rightMax > height[right] ? rightMax : height[right]; max += leftMax < rightMax ? leftMax - height[left++] : rightMax - height[right--]; } return max; } }
Sim Prodigy

public class Solution { public int trap(int[] height) { int l = height.length; if(l < 3) return 0; int[] leftMax = new int[l]; int[] rightMax = new int[l]; int maxL = height[0]; int maxR = height[l-1]; for(int i = 0; i maxL ? height[i] : maxL; leftMax[i] = maxL; maxR = height[l-1-i] > maxR ? height[l-1-i] : maxR; rightMax[l-1-i] = maxR; } int waterTrapped = 0; for(int i = 0; i rightMax[i] ? rightMax[i] - height[i] : leftMax[i] - height[i]; } return waterTrapped; } }
Vasyl Grygoryev

Constant O(1) space and O(n) time.
public class Solution { public int trap(int[] height) { if (height == null || height.length < 3) return 0;
int result = 0; int left = 0; int right = height.length - 1; int maxLeft = 0; int maxRight = 0; int curHeight; while (left < right) { curHeight = Math.min(maxLeft, maxRight); if (maxLeft < maxRight) { result += Math.max(curHeight - height[left], 0); maxLeft = Math.max(height[left], maxLeft); left++; } else { result += Math.max(curHeight - height[right], 0); maxRight = Math.max(height[right], maxRight); right--; } } curHeight = Math.min(maxLeft, maxRight); result += Math.max(curHeight - height[right], 0);
return result; } }
JY

sorry….my mistake….I meant constant space….
JY

Is it possible to do it in constant time? it’s a FB interview question. Haven’t figured out how to do it…

LeetCode – Trapping Rain Water (Java)

Related posts: