LeetCode – Counting Bits (Java)

by

Given a non negative integer number num. For every numbers i in the range 0 ≤ i ≤ num calculate the number of 1’s in their binary representation and return them as an array.

Example:

For num = 5 you should return [0,1,1,2,1,2].

1. Naive Solution

We can simply count bits for each number like the following:

public int[] countBits(int num) {
    int[] result = new int[num+1];
 
    for(int i=0; i<=num; i++){
        result[i] = countEach(i);
    }
 
    return result;
}
 
public int countEach(int num){
    int result = 0;
 
    while(num!=0){
        if(num%2==1){
            result++;
        }
        num = num/2;
    }
 
    return result;
}

2. Improved Solution

For number 2(10), 4(100), 8(1000), 16(10000), …, the number of 1’s is 1. Any other number can be converted to be 2^m + x. For example, 9=8+1, 10=8+2. The number of 1’s for any other number is 1 + # of 1's in x.

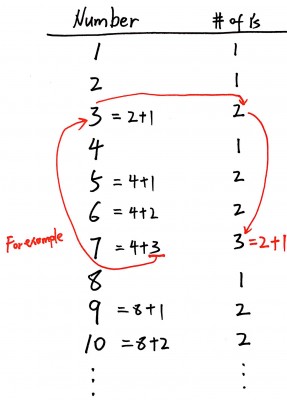
Counting Bits (Java)

public int[] countBits(int num) {
    int[] result = new int[num+1];
 
    int p = 1; //p tracks the index for number x
    int pow = 1;
    for(int i=1; i<=num; i++){
        if(i==pow){
            result[i] = 1;
            pow <<= 1;
            p = 1;
        }else{
            result[i] = result[p]+1;
            p++;
        }
 
    }
 
    return result;
}

3 thoughts on “LeetCode – Counting Bits (Java)”

  1. This question can be solved using DP with Bitmasking.

    The basic intuition behind bottom-up approach is that we are going to
    directly access number of set bits in the number having value
    current_number/2 and we are also going to check whether last bit is set
    in this current_number or not by just doing and operation with 1.

    current_number/2 or current_number>>1 basically removes the last bit of this
    current_number so to include that bit in our count we have to manually
    check the last bit of this number using & operation.

    This would be expression for computing number of set bits in a number i

    dp[i]=dp[i>>1]+(i&1)

    If you still get stuck while solving this question then you can refer to the following video for better explanation.

    Video Link: https://www.youtube.com/watch?v=xnmbO3lxhRM

  2. class Solution {
    public:
    int dp[100000];
    int bits(int n) {
    if(n == 0 || n == 1) {
    return n;
    }

    if(dp[n] != -1) {
    return dp[n];
    }
    // closest 2^n
    int k = 1;
    while((k << 1) <= n) {
    k = k << 1;
    }

    return dp[n] = 1+bits(n-k);

    }

    vector countBits(int num) {
    vector res;
    memset(dp, -1, sizeof(dp));
    for(int i = 0; i <= num; i++) {
    res.push_back(bits(i));
    }
    return res;
    }
    };

  3. public int[] countBits(int num) {
    int [] f = new int[num+1];

    if (num == 0) {
    return f;
    }

    f[1] = 1;
    int lastPowerOfTwo = 0;

    for (int i=2; i<f.length; i++) {
    if ((i & (i-1)) == 0) { // power of 2
    f[i] = 1;
    lastPowerOfTwo = i;
    } else {
    f[i] = 1 + f[i-lastPowerOfTwo];
    }
    }

    return f;
    }

Leave a Comment