Analysis
This problem can be easily solved if the three self crossing cases are summarized well. Here are the three self crossing cases. There are no other self crossing situations based on the restrictions of counter-clockwise.
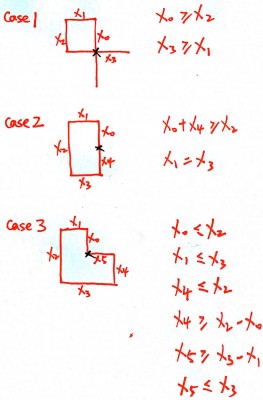
Java Solution
Writing the solution is straightforward once the 3 self crossing cases are identified.
public boolean isSelfCrossing(int[] x) { if(x==null || x.length<=3) return false; for(int i=3; i<x.length; i++){ if(x[i-3] >= x[i-1] && x[i-2]<=x[i]){ return true; } if(i>=4 && x[i-4]+x[i]>=x[i-2] && x[i-3]==x[i-1]) { return true; } if(i>=5 && x[i-5]<=x[i-3] && x[i]<=x[i-2]&& x[i-1]<=x[i-3] && x[i-4]<=x[i-2] && x[i-1]>=x[i-3]-x[i-5] && x[i]>=x[i-2]-x[i-4]){ return true; } } return false; } |
I think there can be more scenarios. what do you think?