Given an integer array nums, find the sum of the elements between indices i and j (i ≤ j), inclusive. The update(i, val) function modifies nums by updating the element at index i to val.
Java Solution 1 – Segment Tree
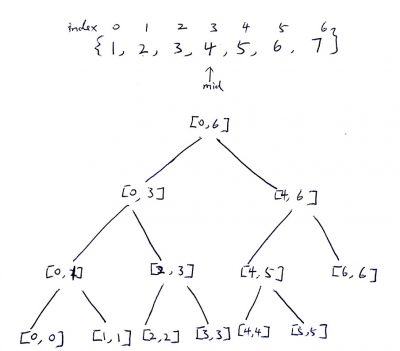
class TreeNode{ int start; int end; int sum; TreeNode leftChild; TreeNode rightChild; public TreeNode(int left, int right, int sum){ this.start=left; this.end=right; this.sum=sum; } public TreeNode(int left, int right){ this.start=left; this.end=right; this.sum=0; } } public class NumArray { TreeNode root = null; public NumArray(int[] nums) { if(nums==null || nums.length==0) return; this.root = buildTree(nums, 0, nums.length-1); } void update(int i, int val) { updateHelper(root, i, val); } void updateHelper(TreeNode root, int i, int val){ if(root==null) return; int mid = root.start + (root.end-root.start)/2; if(i<=mid){ updateHelper(root.leftChild, i, val); }else{ updateHelper(root.rightChild, i, val); } if(root.start==root.end&& root.start==i){ root.sum=val; return; } root.sum=root.leftChild.sum+root.rightChild.sum; } public int sumRange(int i, int j) { return sumRangeHelper(root, i, j); } public int sumRangeHelper(TreeNode root, int i, int j){ if(root==null || j<root.start || i > root.end ||i>j ) return 0; if(i<=root.start && j>=root.end){ return root.sum; } int mid = root.start + (root.end-root.start)/2; int result = sumRangeHelper(root.leftChild, i, Math.min(mid, j)) +sumRangeHelper(root.rightChild, Math.max(mid+1, i), j); return result; } public TreeNode buildTree(int[] nums, int i, int j){ if(nums==null || nums.length==0|| i>j) return null; if(i==j){ return new TreeNode(i, j, nums[i]); } TreeNode current = new TreeNode(i, j); int mid = i + (j-i)/2; current.leftChild = buildTree(nums, i, mid); current.rightChild = buildTree(nums, mid+1, j); current.sum = current.leftChild.sum+current.rightChild.sum; return current; } } |
Java Solution 2 – Binary Index Tree / Fenwick Tree
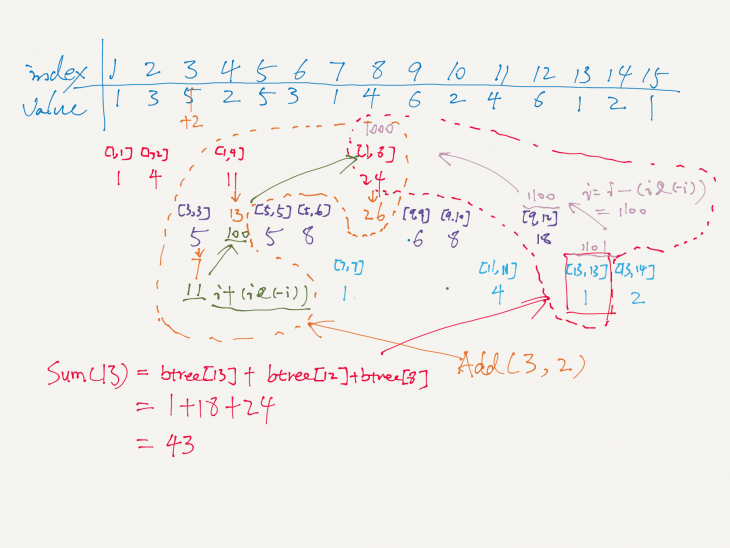
Here is a perfect video to show how binary index tree works. In addition, my notes at the end of the post may also help.
public class NumArray { int[] btree; int[] arr; public NumArray(int[] nums) { btree = new int[nums.length+1]; arr = nums; for(int i=0; i<nums.length; i++){ add(i+1, nums[i]); } } void add(int i, int val) { for(int j=i; j<btree.length; j=j+(j&(-j)) ){ btree[j] += val; } } void update(int i, int val) { add(i+1, val-arr[i]); arr[i]=val; } public int sumRange(int i, int j) { return sumHelper(j+1)-sumHelper(i); } public int sumHelper(int i){ int sum=0; for(int j=i; j>=1; j=j-(j&(-j))){ sum += btree[j]; } return sum; } } |